১। চিত্রে, CD, AB এর লম্ব সমদ্বিখণ্ডক, প্রমাণ কর যে ADC ≅ ∠BDC

২। চিত্রে, CD = CB এবং ∠DCA = ∠BCA প্রমাণ কর যে, AB = AD

৩। চিত্রে, ∠BAC = ∠ACD এবং AB = DC প্রমাণ কর যে, AD = BC, ∠CAD = ∠ACB এবং ∠ADC = ∠ABC
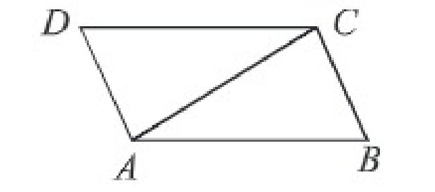
৪। প্রমাণ কর যে, সমদ্বিবাহু ত্রিভুজের সমান বাহু বাদে অপর বাহু উভয়দিকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ দুটি পরস্পর সমান।
৫। চিত্রে, AD = AE, BD = CE এবং ∠AEC = ∠ADB প্রমাণ কর যে, AB = AC
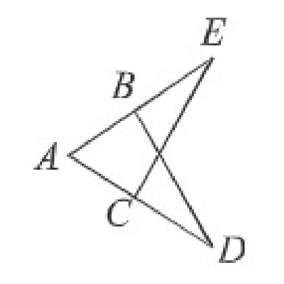
৬। চিত্রে, ∆ABC এবং ∆DBC দুটি সমদ্বিবাহু ত্রিভুজ। প্রমাণ কর যে, ∆ABD = AACD
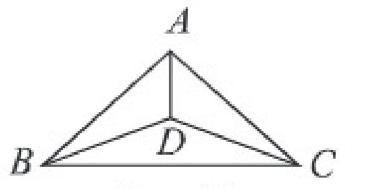
৭। প্রমাণ কর যে, সমদ্বিবাহু ত্রিভুজের ভূমির প্রান্তবিন্দু থেকে বিপরীত বাহুদ্বয়ের উপর অঙ্কিত মধ্যমাদ্বয় সমান।
৮। প্রমাণ কর যে, সমবাহু ত্রিভুজের কোণগুলো পরস্পর সমান।
উপপাদ্য ৩ (বাহু-বাহু-বাহু উপপাদ্য)
যদি একটি ত্রিভুজের তিন বাহু যথাক্রমে অপর একটি ত্রিভুজের তিন বাহুর সমান হয়, তবে ত্রিভুজ দুটি সর্বসম হবে।
বিশেষ নির্বচন: মনে করি, ∆ABC এবং ∆DEF এ AB = DE, AC = DF এবং BC = EF, প্রমাণ করতে হবে যে, ∆ABC ≅ ∆DEF
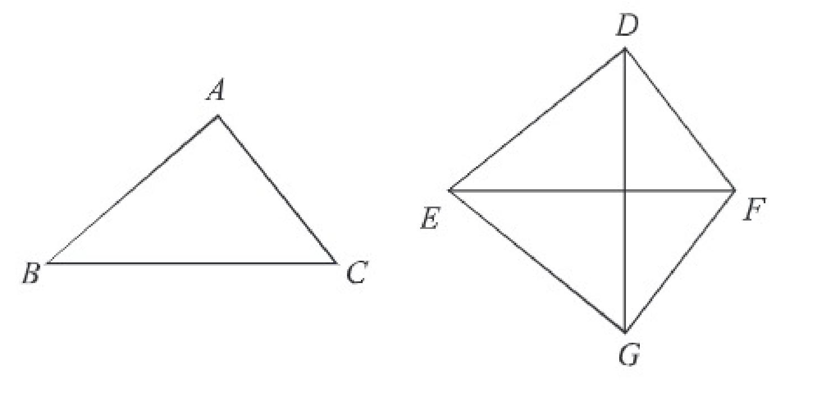
প্রমাণ: মনে করি, BC এবং EF বাহু যথাক্রমে ∆ABC এবং ∆DEF এর বৃহত্তম বাহুদ্বয়।
এখন ∆ABC কে ∆DEF এর উপর এমনভাবে স্থাপন করি, যেন B বিন্দু E বিন্দুর উপর ও BC বাহু EF বাহু বরাবর এবং EF রেখার যে পাশে D বিন্দু আছে, A বিন্দু এর বিপরীত পাশে পড়ে। মনে করি, G বিন্দু A বিন্দুর নতুন অবস্থান।
যেহেতু BC = EF, Cবিন্দু F বিন্দুর উপর পড়বে। সুতরাং ∆GEF হবে ∆ABC এর নতুন অবস্থান। অর্থাৎ, EG = BA, FG=CA ও ∠EGF = ∠BAC D, G যোগ করি।
| ধাপ | যথার্থতা |
| (১) ∆EGD এ EG = ED [কারণ EG = BA = ED] অতএব, ∠EDG = ∠EGD | [ত্রিভুজের সমান বাহুদ্বয়ের বিপরীত কোণ পরস্পর সমান] |
| (২) ∆FGD এ FG = FD অতএব, ∠FDG = ∠FGD | [ত্রিভুজের সমান বাহুদ্বয়ের বিপরীত কোণদ্বয় পরস্পর সমান। |
(৩) সুতরাং, ∠EDG + ∠FDG = ∠EGD + ∠FGD বা, ∠EDF = ∠EGF অর্থাৎ, ∠BAC = ∠EDF ∴∆ABC = ∆DEF (প্রমাণিত)। | [বাহু-কোণ-বাহু উপপাদ্য] |
উপপাদ্য ৪ (কোণ-বাহু-কোণ উপপাদ্য)
যদি একটি ত্রিভুজের দুটি কোণ ও কোণ সংলগ্ন বাহু যথাক্রমে অপর একটি ত্রিভুজের দুটি কোণ ও কোণ সংলগ্ন বাহুর সমান হয়, তবে ত্রিভুজ দুটি সর্বসম হবে।
বিশেষ নির্বচন: মনে করি, ∆ABC = ∆DEF -এ ∠B∠E, ∠C = ∠F এবং কোণ সংলগ্ন BC বাহু = অনুরূপ EF বাহু।

প্রমাণ করতে হবে যে, ∆ABC = ∆DEF
প্রমাণ
| ধাপ | যথার্থতা |
(১) ∆ABC কে ADEF এর উপর এমনভাবে স্থাপন করি যেন, B বিন্দু E বিন্দুর উপর ও BC বাহু EF বাহু বরাবর এবং EF রেখার যে পাশে D আছে বিন্দু A বিন্দু যেন ঐপাশে পড়ে। যেহেতু BC = EF, অতএব C বিন্দু F বিন্দুর উপর অবশ্যই পড়বে। | [ বাহুর সর্বসমতা] |
| (২) আবার, ∠B = ∠E বলে, BA বাহু ED বাহু বরাবর পড়বে এবং ∠C=∠F বলে, CA বাহু FD বাহু বরাবর পড়বে। | |
(৩)∴ BA এবং CA বাহুর সাধারণ বিন্দু A, ED ও FD বাহুর সাধারণ বিন্দু D এর উপর পড়বে। অর্থাৎ, ∆ABC, ∆DEF এর উপর সমাপতিত হবে। ∴∆ABC ≅ ∆DEF (প্রমাণিত)। | [ কোণের সর্বসমতা] |
অনুসিদ্ধান্ত: একটি ত্রিভুজের একটি বাহু ও দুটি কোণ যথাক্রমে অপর একটি ত্রিভুজের একটি বাহু ও দুটি কোণের সমান হলে ত্রিভুজ দুটি সর্বসম।
কাজ 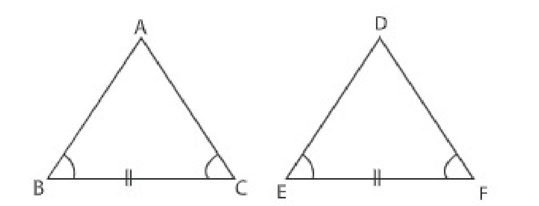 ∆ ABC ও ∆DEF এ BC=EF এবং ∠B=∠E ও ∠C=∠F হলে দেখাও যে, △ ABC ≅ ∆DEF ইঙ্গিত: ∠A+B+C= ∠D+∠E+∠F = ২ সমকোণ হবে। ∴ ∠B=∠E, ∠C=∠F, হলে ∠A=∠D হবে। অতঃপর উপপাদ্য 8 প্রয়োগ কর। |
উদাহরণ ১। প্রমাণ কর যে, কোনো ত্রিভুজের শিরঃকোণের সমদ্বিখণ্ডক যদি ভূমির উপর লম্ব হয়, তবে ত্রিভুজটি সমদ্বিবাহু।
বিশেষ নির্বচন: চিত্রে, ∆ABC এর শিরঃকোণ A-এর সমদ্বিখণ্ডক AD যা ভূমি BC এর D বিন্দুতে লম্ব। প্রমাণ করতে হবে যে, AB = AC
প্রমাণ: ∆ABD এবং ∆ACD এ ∠BAD = ∠CAD [∵AD, ∠BAC এর সমদ্বিখণ্ডক]
∠ADB = ∠ADC [: AD, BC এর উপর লম্ব]
এবং AD সাধারণ বাহু।
সুতরাং ∆ABD ≅ ∆ACD [কোণ বাহু কোণ উপপাদ্য। এতএব, AB = AC [প্রমাণিত]

উপপাদ্য ৫ (সমকোণী অতিভুজ-বাহু উপপাদ্য)
দুটি সমকোণী ত্রিভুজের অতিভুজদ্বয় সমান হলে এবং একটির এক বাহু অপরটির অপর এক বাহুর সমান হলে, ত্রিভুজদ্বয় সর্বসম হবে।

বিশেষ নির্বচন: মনে করি, ABCও DEF সমকোণী ত্রিভুজদ্বয়ে অতিভুজ AC =অতিভুজ DF এবং AB = DE প্রমাণ করতে হবে যে, ∆ABC ≅ ∆DEF
| ধাপ | যথার্থতা |
| (১) ∆ABC কে △DEF এর উপর এমনভাবে স্থাপন করি যেন, B বিন্দু E বিন্দুর উপর, BA বাহু ED বাহু বরাবর এবং C বিন্দু DE এর যে পাশে F বিন্দু আছে এর বিপরীত পাশে পড়ে। ধরি, C বিন্দুর নতুন অবস্থান G। | [ত্রিভুজের দুই বাহু সমান হলে তাদের বিপরীত কোণ দুটি পরস্পর সমান] |
| (২) যেহেতু AB=DE, A বিন্দু D বিন্দুর উপর পড়বে। ফলে △ DEG হবে ∆ABC এর নতুন অবস্থান অর্থাৎ DG AC, ∠G=∠C ∠DEG= ∠B = 1 সমকোণ। | |
(৩) যেহেতু ∠DEF+∠DEG = 1 সমকোণ + 1 সমকোণ = 2 সমকোণ = 1 সরলকোণ, GEF একটি সরলরেখা। সুতরাং △ DGF একটি সমদ্বিবাহু ত্রিভুজ। যার DG=DF ∴ ∠FZG=∠C | [কোণ-বাহু-কোণ উপপাদ্য |
| (৪) এখন △ ABC ও △DEF এর ∠B = ∠E [প্রত্যেকে ১ সমকোণ। ∠C = ∠F এবং AB = অনুরূপ DE সুতরাং △ ABC ≅ △DEF (প্রমাণিত) |
common.read_more